I
Пло́щадь
одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины.
Вычисление П. было уже в древности одной из важнейших задач практической геометрии (разбивка земельных участков). За несколько столетий до нашей эры греческие учёные располагали точными правилами вычисления П., которые в "Началах" Евклида (См.
Начала Евклида) облечены в форму теорем. При этом П. многоугольников определялись теми же приёмами разложения и дополнения фигур, какие сохранились в школьном преподавании. Для вычисления П. фигур с криволинейным контуром применялся предельный переход в форме
Исчерпывания метода
. Теория П. плоских фигур, ограниченных простыми (т. е. не пересекающими себя) контурами, может быть построена следующим образом. Рассматриваются всевозможные многоугольники, вписанные в фигуру
F, и всевозможные многоугольники, описанные вокруг фигуры
F. (Вычисление П. многоугольника сводится к вычислению П. равновеликого ему квадрата, который может быть получен посредством надлежащих прямолинейных разрезов и перекладывания полученных частей.) Пусть
{Si} - числовое множество П. вписанных в фигуру многоугольников, a
{Sd} - числовое множество П. описанных вокруг фигуры многоугольников. Множество
{Si} ограничено сверху (площадью любого описанного многоугольника), а множество
{Sd} ограничено снизу (например, числом нуль). Наименьшее из чисел
 ,
, ограничивающее сверху множество
{Si}, называется нижней площадью фигуры
F, а наибольшее из чисел
, ограничивающее снизу множество
{Sd}, называется верхней площадью фигуры
F. Если верхняя П. фигуры совпадает с её нижней П., то число S =
называется площадью фигуры, а сама фигура - квадрируемой фигурой. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры многоугольник и такой вписанный в фигуру многоугольник, разность
Sd-Si площадей которых была бы меньше ε.
Аналитически П. плоской фигуры может быть вычислена с помощью интегралов. Пусть фигура F - т. н. криволинейная трапеция (рис. 1) - ограничена графиком заданной на сегменте [a, b] непрерывной и неотрицательной функции f (x), отрезками прямых х = а и х = b и отрезком оси Ox между точками (а, 0) и (b, 0). П. такой фигуры может быть выражена интегралом
.
П. фигуры, ограниченной замкнутым контуром, который встречается с параллелью к оси Оу не более чем в двух точках, может быть вычислена как разность П. двух фигур, подобных криволинейной трапеции. П. фигуры может быть выражена в виде двойного интеграла:
,
где интегрирование распространяется на часть плоскости, занятой фигурой.
Теория П. фигур, расположенных на кривой поверхности, может быть определена следующим образом. Пусть F - односвязная фигура на гладкой поверхности, ограниченная кусочно гладким контуром. Фигура F разбивается кусочно гладкими кривыми на конечное число частей Фi, каждая из которых однозначно проектируется на касательную плоскость, проходящую через точку Mi, принадлежащую части Фi, (рис. 2). Предел сумм площадей этих проекций (если он существует), взятых по всем элементам разбиения, при условиях, что максимум диаметров этих элементов стремится к нулю и что он не зависит от выбора точек Mi, называется площадью фигуры F. Фигура на поверхности, для которой этот предел существует, называется квадрируемой. Квадрируемыми являются кусочно гладкие ограниченные полные двусторонние поверхности. П. всей поверхности слагается из П. составляющих её частей.
Аналитически П. фигуры F на поверхности, заданной уравнением z = f (x, у), где функция f однозначна и имеет непрерывные частные производные, может быть выражена следующим образом
.
Здесь G - замкнутая область, являющаяся проекцией фигуры F на плоскость Оху, ds - элемент площади на поверхности.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1-2, М., 1970; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1-2, М., 1971-73.
Рис. 1 к ст. Площадь.
Рис. 2 к ст. Площадь.
II
Пло́щадь
открытое, архитектурно организованное, обрамленное какими-либо зданиями, сооружениями или зелёными насаждениями пространство, входящее в систему других городских пространств. Предшественниками городских П. были парадные дворы дворцовых и храмовых комплексов Крита, Египта, Вавилонии, Ассирии. Их прямоугольный план и периметрическую застройку унаследовали древнегреческие агоры (См.
Агора) и древнеримские
Форумы
. Столь же замкнутый характер (при почти всегда нерегулярном плане) имели П. европейских городов 12-14 вв.; главные П. были торговые П. В эпоху Возрождения создавались обычно П. с очертаниями в виде правильной геометрической фигуры (прямоугольник, трапеция); большое значение приобрели П. для гражданских собраний со зданием городского управления и лоджией (См.
Лоджия)
для заседаний патрициата.
Барокко вводит в практику градостроительства круглые, многоугольные и сложных очертаний П.
Большую общественную и градостроительную роль играли кремлёвские, торговые, соборные П. в русских средневековых городах. В 18 в. получили широкое распространение П. с открытой пространственной композицией. Выдающиеся образцы П. различного назначения были созданы архитекторами русского классицизма в последней трети 18 - 1-й трети 19 вв.
В современном градостроительстве городские П. делятся на два типа: транспортные и пешеходные. Транспортные П. выполняют функции узлов движения городского транспорта; П. с большой интенсивностью движения иногда сооружают в нескольких ярусах (на поверхности земли, подземные, надземные) для развязки движения транспорта в разных уровнях. Транспортные П. часто имеют конкретное специализированное назначение: например, вокзальные П. (на которых должны быть разделены потоки пассажиров, направляющихся на посадку и прибывающих), П. с обширными стоянками автомобилей перед крупными заводами, стадионами, зрелищными и выставочными сооружениями (на таких П. должны быть разделены потоки людей, направляющихся на работу или в зрелищные учреждения, и потоки людей, возвращающихся обратно). П., предназначенные преимущественно для движения пешеходов, также могут иметь специализированное назначение: главные П. - парадный и представительный центр города, театральные, торговые, мемориальные (в честь больших исторических событий, выдающихся государственных деятелей, учёных, мастеров искусства). Такие П., в композицию которых зачастую включаются произведения монументальной скульптуры и живописи, иногда являются выдающимися архитектурными ансамблями и в значительной мере определяют облик населённых мест. Главные П. или системы главных П., являющиеся ядром центра города, обычно имеют большие размеры и наиболее впечатляющую, монументальную застройку (например, здания общегосударственных и городских учреждений); здесь проводятся парады, праздничные демонстрации, митинги, народные гуляния. В современном градостроительстве вблизи парадных, главных П., на которых размещены здания, привлекающие значительное число работающих, зрителей, посетителей и пр., размещают специальные транспортные П. для временной стоянки автомобилей. П. различного назначения могут иметь озеленение в центральной части (преимущественно партерное; см.
Партер) или по периметру, либо смешанное. В садово-парковых П. партерная часть обычно сочетается с деревьями и кустарниками, кронам которых стрижкой придают определённую геометрическую форму, или с естественными куртинами зелёных массивов, обрамляющих П. См. также статьи
Градостроительство, Дворцовая площадь, Искусств площадь, Красная площадь, Марсово поле, Островского площадь. Лит.: Брикман А. Э., Площадь и монумент как проблема художественной формы, М., 1935; Бунин А. В., История градостроительного искусства, т. 1, М., 1953; Баранов Н. В., Композиция центра города, [М., 1964]; Основы советского градостроительства, т. 2, 4, М., 1967-69.
Н. В. Баранов.
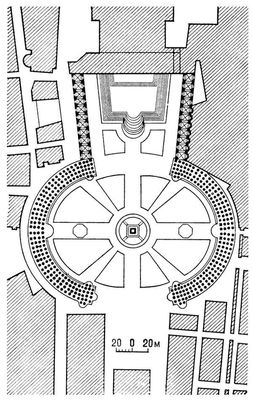
Площадь св. Петра в Риме. 1657-63. Архитектор Л. Бернини. План.
Ансамбль площади Островского и улицы зодчего Росси в Ленинграде. 1816-34. Архитектор К. И. Росси. План.
Н. де Шатийон. Королевская площадь (ныне площадь Вогезов) в Париже. 1606-2 (фрагмент из плана Тюрго. 1734-39). Обстроена зданиями с одинаковыми фасадами. В центре монумент Людовика XIII.
Планы площадей в городах Западной Европы в 16-19 вв. 1. Пьяцца делла Синьория во Флоренции: а - Палаццо делла Синьория (начато в 1298); б - улица Уффици (1560-1585); в - Лоджия деи Ланци (около 1376-80); г - статуя "Давид" (1501-04); д - фонтан Нептуна (1575). 2. Пьяцца Сан-Марко и Пьяццетта в Венеции: а - собор Сан-Марко (829-832, перестроен в 1073-95); б - Дворец дожей (строился с 9 в.); в - Старая библиотека Сан-Марко (1536-54, окончена в 1583); г - кампанила (888-1517); д - Старые Прокурации (1480 и 1511-14); е - Новые Прокурации (1584-1611 и 1640); ж - колонны из гранитных монолитов, привезённых в 1127 из Египта. 3. Пьяцца Санта-Мария делла Паче в Риме. Середина 17 в. Архитектор Пьетро да Кортона (1 - церковь Санта-Мария делла Паче, 1480-е гг.).

Планы площадей в городах Западной Европы в 16-19 вв. 4. Пьяцца дель Пополо в Риме: 1-1 - улица Виа дель Корсо (восходит к античному периоду); 2-2 - улица Виа дель Бабуино (проложена в 1534-49); 3-3 - улица Виа ди Рипетта (пробита в 1513-21); 4 - обелиск (1589); 5 - церковь Санта-Мария деи Мираколи (1662); 6 - церковь Санта-Мария ин Монте Санто (1662); 7 - рампы (1816-20); 8 - терраса Пинчо (1816-20). 5. Королевская площадь (ныне площадь Биржи) в Бордо. 1728. Архитекторы Ж. Габриель и Ж. А. Габриель (1 - набережная; 2 - монумент Людовика XV)